Bagging and Boosting are similar in that they are both ensemble techniques, where a set of weak learners are combined to create a strong learner that obtains better performance than a single one.
ENSEMBLE LEARNING
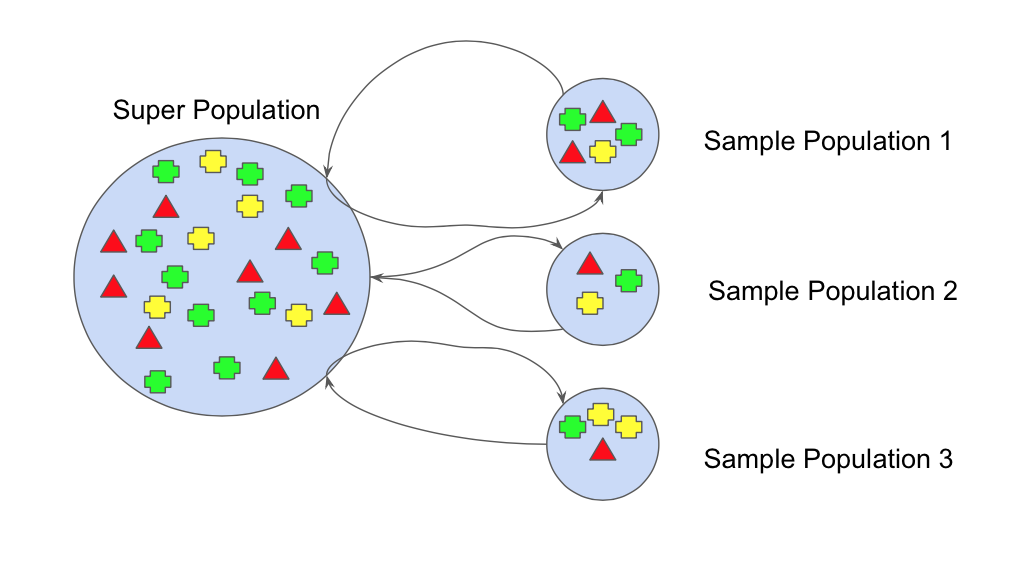
Ensemble methods combine several decision trees classifiers to produce better predictive performance than a single decision tree classifier. The main principle behind the ensemble model is that a group of weak learners come together to form a strong learner, thus increasing the accuracy of the model.When we try to predict the target variable using any machine learning technique, the main causes of difference in actual and predicted values are noise, variance, and bias. Ensemble helps to reduce these factors (except noise, which is irreducible error).
Another way to think about Ensemble learning is Fable of blind men and elephant. All of the blind men had their own description of the elephant. Even though each of the description was true, it would have been better to come together and discuss their undertanding before coming to final conclusion. This story perfectly describes the Ensemble learning method.
Using techniques like Bagging and Boosting helps to decrease the variance and increased the robustness of the model. Combinations of multiple classifiers decrease variance, especially in the case of unstable classifiers, and may produce a more reliable classification than a single classifier.
But before understanding Bagging and Boosting and how different classifiers are selected in the two algorithms, lets first talk about Bootstrapping.
BOOTSTRAPPING
Bootstrap refers to random sampling with replacement. Bootstrap allows us to better understand the bias and the variance with the dataset. Bootstrap involves random sampling of small subset of data from the dataset. This subset can be replace. The selection of all the example in the dataset has equal probability. This method can help to better understand the mean and standand deviation from the dataset.
Let’s assume we have a sample of ‘n’ values (x) and we’d like to get an estimate of the mean of the sample.
mean(x) = 1/n * sum(x)
We know that our sample is small and that our mean has error in it. We can improve the estimate of our mean using the bootstrap procedure:
- Create many (e.g. m) random sub-samples of our dataset with replacement (meaning we can select the same value multiple times).
- Calculate the mean of each sub-sample.
- Calculate the average of all of our collected means and use that as our estimated mean for the data.
For example, let’s say we used 3 resamples and got the mean values 2.5, 3.3 and 4.7. Taking the average of these we could take the estimated mean of the data to be 3.5.
Having understood Bootstrapping we will use this knowledge to understand Bagging and Boosting.
BAGGING
Bootstrap Aggregation (or Bagging for short), is a simple and very powerful ensemble method. Bagging is the application of the Bootstrap procedure to a high-variance machine learning algorithm, typically decision trees.
- Suppose there are N observations and M features. A sample from observation is selected randomly with replacement(Bootstrapping).
- A subset of features are selected to create a model with sample of observations and subset of features.
- Feature from the subset is selected which gives the best split on the training data.(Visit my blog on Decision Tree to know more of best split)
- This is repeated to create many models and every model is trained in parallel
- Prediction is given based on the aggregation of predictions from all the models.
When bagging with decision trees, we are less concerned about individual trees overfitting the training data. For this reason and for efficiency, the individual decision trees are grown deep (e.g. few training samples at each leaf-node of the tree) and the trees are not pruned. These trees will have both high variance and low bias. These are important characterize of sub-models when combining predictions using bagging. The only parameters when bagging decision trees is the number of samples and hence the number of trees to include. This can be chosen by increasing the number of trees on run after run until the accuracy begins to stop showing improvement
BOOSTING
Boosting refers to a group of algorithms that utilize weighted averages to make weak learners into stronger learners. Unlike bagging that had each model run independently and then aggregate the outputs at the end without preference to any model. Boosting is all about “teamwork”. Each model that runs, dictates what features the next model will focus on.
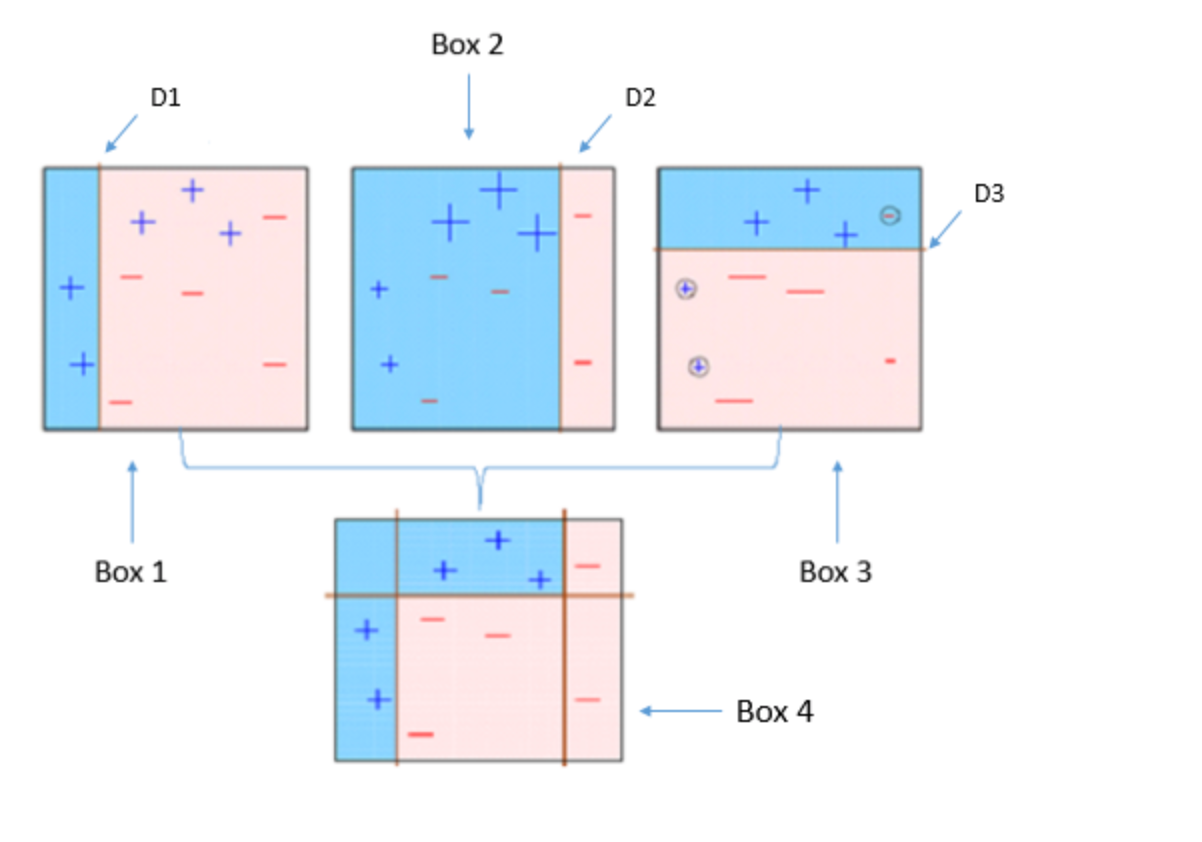
Box 1: You can see that we have assigned equal weights to each data point and applied a decision stump to classify them as + (plus) or — (minus). The decision stump (D1) has generated vertical line at left side to classify the data points. We see that, this vertical line has incorrectly predicted three + (plus) as — (minus). In such case, we’ll assign higher weights to these three + (plus) and apply another decision stump.
Box 2: Here, you can see that the size of three incorrectly predicted + (plus) is bigger as compared to rest of the data points. In this case, the second decision stump (D2) will try to predict them correctly. Now, a vertical line (D2) at right side of this box has classified three mis-classified + (plus) correctly. But again, it has caused mis-classification errors. This time with three -(minus). Again, we will assign higher weight to three — (minus) and apply another decision stump.
Box 3: Here, three — (minus) are given higher weights. A decision stump (D3) is applied to predict these mis-classified observation correctly. This time a horizontal line is generated to classify + (plus) and — (minus) based on higher weight of mis-classified observation.
Box 4: Here, we have combined D1, D2 and D3 to form a strong prediction having complex rule as compared to individual weak learner. You can see that this algorithm has classified these observation quite well as compared to any of individual weak learner.
Which is the best, Bagging or Boosting?
There’s not an outright winner; it depends on the data, the simulation and the circumstances.
Bagging and Boosting decrease the variance of your single estimate as they combine several estimates from different models. So the result may be a model with higher stability.
Bagging and Boosting decrease the variance of your single estimate as they combine several estimates from different models. So the result may be a model with higher stability.
If the problem is that the single model gets a very low performance, Bagging will rarely get a better bias. However, Boosting could generate a combined model with lower errors as it optimises the advantages and reduces pitfalls of the single model.
By contrast, if the difficulty of the single model is over-fitting, then Bagging is the best option. Boosting for its part doesn’t help to avoid over-fitting; in fact, this technique is faced with this problem itself. For this reason, Bagging is effective more often than Boosting.




No comments:
Post a Comment