Confusion Matrix Unplugged !!

Homepag

Confusion Matrix

Confusion matrix also known as error matrix, is the technique for summarising the prediction results of a classification algorithm in machine learning. The matrix table presents the number of correct and incorrect prediction values which helps evaluate the performance of a classification model.

Mostly used for binary classification problems, this serves as an important tool in understanding algorithm/model’s performance in terms of accuracy.

A binary(Yes/No) outcome classification example

• Label e.g Pregnancy Test or Spam Email
• Prediction value — Yes/No

The four types of prediction mistakes or errors a Classifier model might make -

1. True label is Positive, Prediction value is Positive = True Positive
2. True label is Negative, Prediction value is Negative = True Negative
3. True label is Positive, Prediction value is Negative = False Negative = or saying pregnant is non-pregnant
4. True label is Negative, Prediction value is Positive = False Positive = or saying that non-pregnant is pregnant

Both false positives and false negatives can have different impacts — Food for thought kind of example from medical world -

e.g. False negative, there is a patient with a life-threatening disease but it didn’t get detected as the classifier predicted it as Negative so it could go untreated.

e.g. False Positive, the patient doesn’t have the disease. But the prediction classified it as positive and the patient can potentially get treated for the disease.

Forward Propagation -Neural Network

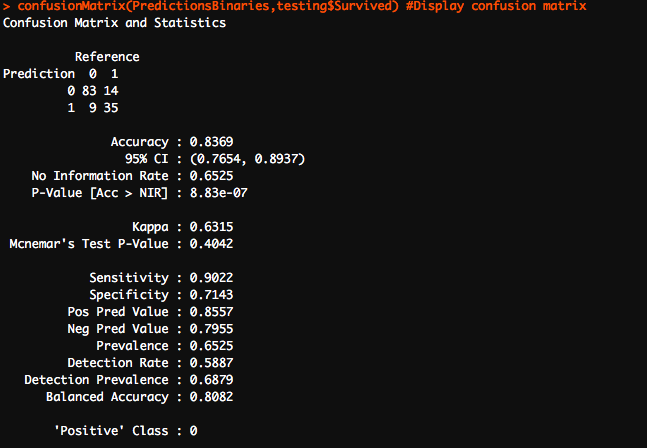
In this blog, we will intuitively understand how a neural network functions and the math behind it with the help of an example. In this example, we will be using a 3-layer network (with 2 input units, 2 hidden layer units, and 2 output units). The network and parameters (or weights) can be represented as follows.

Let us say that we want to train this neural network to predict whether the market will go up or down. For this, we assign two classes Class 0 and Class 1. Here, Class 0 indicates the datapoint where the market closes down, and conversely, Class 1 indicates that the market closes up. To make this prediction, a train data(X) consisting of two features x1, and x2. Here x1 represents the correlation between the close prices and the 10- day simple moving average (SMA) of close prices, and x2 refers to the difference between the close price and the 10-day SMA.

In this example below, the datapoint belongs to the class 1. The mathematical representation of the input data is as follows:

X = [x1, x2] = [0.85,.25] y= [1]

Example with two data points:

The output of the model is categorical or a discrete number. We need to convert this output data also into a matrix form. This enables the model to predict the probability of a datapoint belonging to different classes. When we make this matrix conversion, the columns represent the classes to which that example belongs, and the rows represent each of the input examples.

In the matrix y, the first column represents class 0 and second column represents class 1. Since our example belongs to the Class 1, we have 1 in the second column, and zero in the first.

This process of converting discrete/categorical classes to logical vectors/ matrix is called One Hot Encoding. We use one hot encoding as the neural network cannot operate on label data directly. They require all input variables and output variables to be numeric.

In a neural network, apart from the input variable we add a bias term to every layer other than the output layer. This bias term is a constant, mostly initialized to 1. The bias enables moving the activation threshold along the x-axis.

When the bias is negative the movement is made to the right side, and when the bias is positive the movement is made to the left side. So a biased neuron should be capable of learning even such input vectors that an unbiased neuron is not able to learn. In the dataset X, to introduce this bias we add a new column denoted by ones, as shown below.

Let us visualize the neural network, with the bias included in the input layer.

The second layer in the neural network is the hidden layer, which takes the outputs of the first layer as its input. The third layer is the output layer which gives the output of the neural network.

Let us randomly initialize the weights or parameters for each of the neurons in the first layer. As you can see in the diagram we have a line connecting each of the cells in the first layer to the two neurons in the second layer. This gives us a total of 6 weights to be initialized, 3 for each neuron in the hidden layer. We represent these weights as shown below.

Here, Theta1 is the weights matrix corresponding to the first layer.

The first row in the above representation shows the weights corresponding to the first neuron in the second layer, and the second row represents the weights corresponding to the second neuron in the second layer. Now, let’s do the first step of the forward propagation, by multiplying the input value for each example by their corresponding weights which is mathematically show below.

Theta1 * X

Before we go ahead and multiply, we must remember that when you do matrix multiplications, each element of the product, X*Theta, is the dot product sum of the row in the first matrix X with each of the columns of the second matrix Theta1.

When we multiply the two matrices, X and Theta1, we are expected to multiply the weights with the corresponding input example values. This means we need to transpose the matrix of example input data, X, so that the matrix will multiply each weight with the corresponding input correctly.

z2 = Theta1*Xt

Here z2 is the output after matrix multiplication, and Xt is the transpose of X.

The matrix multiplication process:

Let us say that we have applied a sigmoid activation after the input layer. Then we have to element-wise apply the sigmoid function to the elements in the z² matrix above. The sigmoid function is given by the following equation:

f(x) = 1/(1+e-x)

After the application of activation function, we are left with a 2×1 matrix as shown below.

Here a(2) represents the output of the activation layer.

These outputs of the activation layer act as the inputs for the next or the final layer, which is the output layer. Let us initialize another random weights/parameters called Theta2 for the hidden layer. Each row in Theta2 represents the weights corresponding to the two neurons in the output layer.

After initializing the weights (Theta2), we will repeat the same process that we followed for the input layer. We will add a bias term for the inputs of the previous layer. The a(2) matrix looks like this after the addition of bias vectors:

Let us see how the neural network looks like after the addition of bias unit:

Before we run our matrix multiplication to compute the final output z³, remember that before in z² calculation we had to transpose the input data a¹ to make it “line up” correctly for the matrix multiplication to result in the computations we wanted. Here, our matrices are already lined up the way we want, so there is no need to take the transpose of the a(2) matrix. To understand this clearly, ask yourself this question: “Which weights are being multiplied with what inputs?”.

Now, let us perform the matrix multiplication:

z3 = Theta2*a(2)

where z3 is the output matrix before the application of an activation function.

Here for the last layer, we will be multiplying a 2×3 with a 3×1 matrix, resulting in a 2×1 matrix of output hypotheses. The mathematical computation is shown below:

After this multiplication, before getting the output in the final layer, we apply an element-wise conversion using the sigmoid function on the z² matrix.

a3 = sigmoid(z3)

Where a3 denotes the final output matrix.

The output of a sigmoid function is the probability of the given example belonging to a particular class. In the above representation, the first row represents the probability that the example belonging to Class 0 and the second row represents the probability of Class 1.

As you can see, the probability of example belonging to a Class 1 is lesser than Class 0, which is incorrect and needs to be improved.

Gradient Boosting Machine -Adaboost Quick look

What is Gradient Boosting?

Let’s start by understanding Boosting! Boosting is a method of converting weak learners into strong learners. In boosting, each new tree is a fit on a modified version of the original data set. The gradient boosting algorithm (gbm) can be most easily explained by first introducing the AdaBoost Algorithm.The AdaBoost Algorithm begins by training a decision tree in which each observation is assigned an equal weight. After evaluating the first tree, we increase the weights of those observations that are difficult to classify and lower the weights for those that are easy to classify. The second tree is therefore grown on this weighted data. Here, the idea is to improve upon the predictions of the first tree. Our new model is therefore Tree 1 + Tree 2. We then compute the classification error from this new 2-tree ensemble model and grow a third tree to predict the revised residuals. We repeat this process for a specified number of iterations. Subsequent trees help us to classify observations that are not well classified by the previous trees. Predictions of the final ensemble model is therefore the weighted sum of the predictions made by the previous tree models.

Gradient Boosting trains many models in a gradual, additive and sequential manner. The major difference between AdaBoost and Gradient Boosting Algorithm is how the two algorithms identify the shortcomings of weak learners (eg. decision trees). While the AdaBoost model identifies the shortcomings by using high weight data points, gradient boosting performs the same by using gradients in the loss function (y=ax+b+e, e needs a special mention as it is the error term). The loss function is a measure indicating how good are model’s coefficients are at fitting the underlying data. A logical understanding of loss function would depend on what we are trying to optimise. For example, if we are trying to predict the sales prices by using a regression, then the loss function would be based off the error between true and predicted house prices. Similarly, if our goal is to classify credit defaults, then the loss function would be a measure of how good our predictive model is at classifying bad loans. One of the biggest motivations of using gradient boosting is that it allows one to optimise a user specified cost function, instead of a loss function that usually offers less control and does not essentially correspond with real world applications.

Training a GBM Model in R

In order to train a gbm model in R, you will first have to install and call the gbm library. The gbm function requires you to specify certain arguments. You will begin by specifying the formula. This will include your response and predictor variables. Next, you will specify the distribution of your response variable. If nothing is specified, then gbm will try to guess. Some commonly used distributions include- “bernoulli” (logistic regression for 0–1 outcome), “gaussian” (squared errors), “tdist”(t-distribution loss), and “poisson” (count outcomes). Finally, we will specify the data and the n.trees argument (after all gbm is an ensemble of trees!) By default, the gbm model will assume 100 trees, which can provide is a good estimate of our gbm’s performance.

Training a gbm model on Kaggle’s Titanic Dataset: I have used the famous Titanic data set from Kaggle to illustrate how we can implement a gbm model. I started off by loading the Titanic data into my R Console by using the read.csv() function. The original dataset was then partitioned into separate train and test sets using the createDataPartition() function. This essential split would be extremely useful in the later stages to assess the model’s performance on a separate holdout dataset (Test Data) and to calculate the AUC value. The following screen displays the R code.

Note: Considering the small size of the original dataset, I have assigned 750 observations to the train and 141 observations to the test holdout. Further, by defining a seed value, I have ensured that the same set of random numbers are generated every time. Doing so will remove the uncertainty around the modelling results and help one assess the model’s performance accurately.

The next step is to train a gbm model using our training holdout. While all other arguments are exactly what were discussed in the previous section, there are two additional arguments that have been specified- interaction.depthand shrinkage. Interaction Depth specifies the maximum depth of each tree( i.e. highest level of variable interactions allowed while training the model). Shrinkage is considered as the learning rate. It is used for reducing, or shrinking, the impact of each additional fitted base-learner (tree). It reduces the size of incremental steps and thus penalises the importance of each consecutive iteration.

Note: Even though we are initially training our model with 1000 trees, we can prune the number of trees based on either the “Out-of-Bag or “Cross-Validation” technique to avoid overfitting. We will later see how to incorporate this in our gbm model (see the section “Tuning a gbm model and Early Stopping”)

Understanding the GBM Model Output

When you print a gbm model, it will remind you how many trees or iterations were used in its execution. Using its internal calculations such as Variable Importance, it will also point whether any of the predictor variables had zero influence in the model.

An important feature in the gbm modelling is the Variable Importance. Applying the summary function to a gbm output produces both a Variable Importance Table and a Plot of the model. This table below ranks the individual variables based on their relative influence, which is a measure indicating the relative importance of each variable in training the model. In the Titanic Model, we can see that Cabin and Sex are by far the most important variables in our gbm model.

Tuning a gbm Model and Early Stopping

Hyperparameter tuning is especially significant for gbm modelling since they are prone to overfitting. The special process of tuning the number of iterations for an algorithm such as gbm and random forest is called “Early Stopping”. Early Stopping performs model optimisation by monitoring the model’s performance on a separate test data set and stopping the training procedure once the performance on the test data stops improving beyond a certain number of iterations.

It avoids overfitting by attempting to automatically select the inflection point where performance on the test dataset starts to decrease while performance on the training dataset continues to improve as the model starts to overfit. In the context of gbm, early stopping can be based either on an out of bag sample set (“OOB”) or cross- validation (“cv”). Like mentioned above, the ideal time to stop training the model is when the validation error has decreased and started to stabilise before it starts increasing due to overfitting.

While other boosting algorithms such as “xgboost” allow the user to specify a bunch of metrics such as error and log loss, the “gbm” algorithm specifically uses the metric “error” to evaluate and measure model performance. In order to implement early stopping in “gbm”, we will first have to specify an additional argument called “c.v folds” while training our model. Secondly, the gbm package comes with a default function called gbm.perf() to determine the optimum number of iterations. The argument “method” allows the user to specify the technique used (“OOB” or “cv”) for deciding the optimum number of trees.

The following console screen displays the optimum number of trees as per the “OOB” and “cv” method.

Further, we will also see two plots indicating the optimum number of trees based on the respective technique used. The graph on the left indicates the error on test (green line) and train data set (black line). The blue dotted line points the optimum number of iterations. One can also clearly observe that the beyond a certain a point (169 iterations for the “cv” method), the error on the test data appears to increase because of overfitting. Hence, our model will stop the training procedure on the given optimum number of iterations.

Predictions using gbm

Finally, predict.gbm() function allows to generate the predictions out of the data. One important feature of the gbm’s predict is that the user has to specify the number of trees. Since there is no default value for “n.trees” in the predict function, it is compulsory for the modeller to specify one. Since we have figured out the optimum number of trees by performing early stopping, we will use the optimum values for specifying the “n.trees” argument. I have used the optimum solution based on the cross validation technique as cross validation usually outperforms the OOB method on large datasets. One another argument that the user can specify in the predict function is the type, which controls the type of output generated from the function. In other words, type refers to the scale on which gbm makes predictions.

Concluding and Assessing the Results:

Finally, the most important part of any modelling exercise is to assess the predictions and gauge the model’s performance. I started off by creating a confusion matrix. A really useful tool, the confusion matrix compares the model’s actual values with the predicted values. It is called a confusion matrix because it reveals how confused your model is between the two classes. The columns of the confusion matrix are the true classes while the rows of the matrix are the predicted classes. Before you make your confusion matrix, you need to “cut” your predicted probabilities at a given threshold to turn probabilities into class predictions. You can do this easily with the ifelse()function. In our example, cases with probabilities greater than 0.7 were labelled as 1 i.e likely to survive and cases with lesser probabilities were labelled as 0. Remember calling the “caret” library in order to run the confusion matrix.

Running the last line will produce our confusion matrix.

I am as delighted as you are on seeing the accuracy of our model! Diving deeper into the confusion matrix, we observe that our model perfectly predicted 118 out of 141 observations, giving us an accuracy of 83.69%. There were 23 cases that our model got wrong. These 23 cases were divided between False negatives and false positives as 9 and 14 respectively.

The ROC and the AUC: Based on the true and false positives, I produced the ROC curve and calculated our AUC value.

By definition, the closer the ROC curve comes to the upper left corner in the grid, the better it is. The upper left corner corresponds to a true positive rate of 1 and a false positive rate of 0. This further implies that good classifiers have bigger areas under the curves. As evident, our model has an AUC of 0.8389.

I 282

SHARES